Improving Search with the Levenshtein Algorithm

Recently, I improved the search functionality of my Node.js/Express app by using the Levenshtein algorithm. Here’s how I did it.

Search is one of the most important features of any website. If users can’t find what they’re looking for, they’ll leave — simple as that. But search isn’t always as straightforward as checking if a word exists in a dataset. Typos, plural forms, or slightly different spellings can break exact-match queries. That’s where fuzzy search comes in.

---

What is the Levenshtein Algorithm?

The Levenshtein distance¹ between two strings $|a|$ and $|b|$ is defined recursively as:

$$d_{lev}(a, b) = \begin{cases} |a| & \text{if } |b| = 0 \\ |b| & \text{if } |a| = 0 \\ \min \begin{cases} d_{lev}(a_{1..i-1}, b_{1..j}) + 1 & \text{(deletion)} \\ d_{lev}(a_{1..i}, b_{1..j-1}) + 1 & \text{(insertion)} \\ d_{lev}(a_{1..i-1}, b_{1..j-1}) + [a_i \neq b_j] & \text{(substitution)} \end{cases} \end{cases}$$

where:

• $|a|$ and $|b|$ denote the lengths of strings $a$ and $b$,
• $(a_i \neq b_j)$ is $0$ if the characters match, and $1$ otherwise.

In simpler terms: the distance is the minimum number of edits (insertions, deletions, substitutions) needed to transform one word into the other.

---

Examples

1. Basic substitution:

   $$d_{lev}(\text{"kitten"}, \text{"sitting"}) = 3$$

   Edits: $k \to s$, $e \to i$, $\varepsilon \to g$.

---

2. Insertion + deletion:

   $$d_{lev}(\text{"flaw"}, \text{"lawn"}) = 2$$

   Edits: $k \to s$, $e \to i$, $\varepsilon \to g$.

---

3. Mixed operations:

   $$d_{lev}(\text{"gumbo"}, \text{"gambol"}) = 2$$

   Edits: $u \to a$, $\varepsilon \to l$.

---

4. Exact match case:

   $$d_{lev}(\text{"search"}, \text{"search"}) = 0$$

   No edits needed.

---

5. Longer word variation:

   $$d_{lev}(\text{"saturday"}, \text{"sunday"}) = 3$$

   Edits: $a \to \varepsilon$, $t \to \varepsilon$, $r \to n$.

---

This definition might look math-heavy, but in practice it boils down to filling out a matrix of partial distances. Let’s see how that looks in JavaScript.

---

Implementing Levenshtein in JavaScript

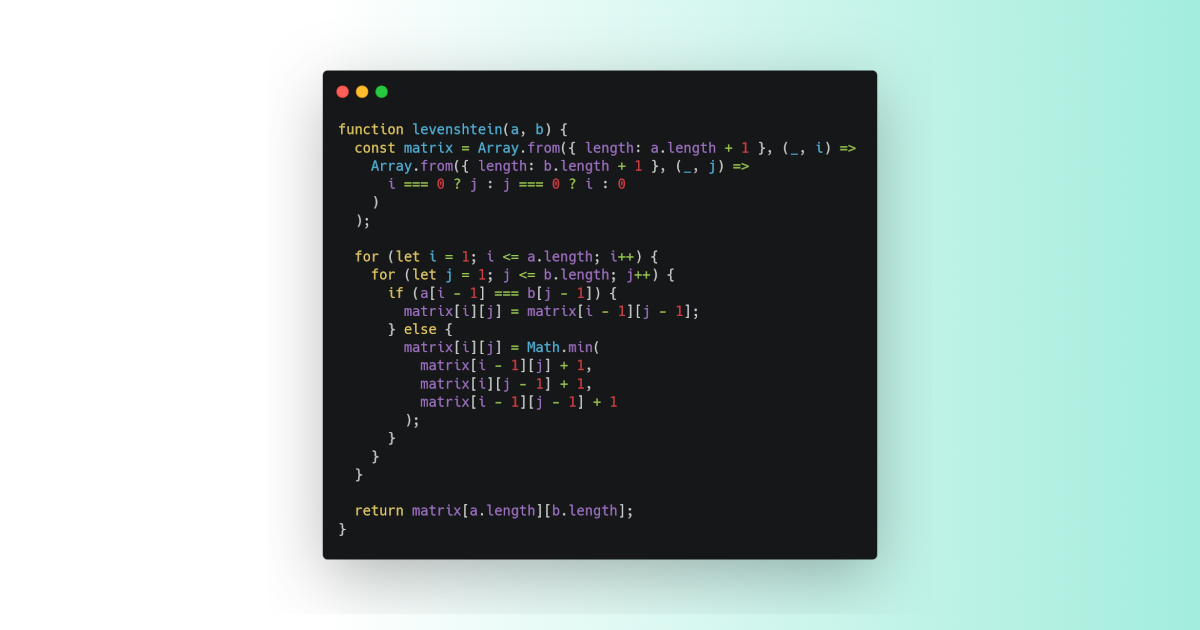
Here’s a simple, dynamic programming implementation:

function levenshtein(a, b) {
  const matrix = Array.from({ length: a.length + 1 }, (_, i) =>
    Array.from({ length: b.length + 1 }, (_, j) =>
      i === 0 ? j : j === 0 ? i : 0
    )
  );

  for (let i = 1; i <= a.length; i++) {
    for (let j = 1; j <= b.length; j++) {
      if (a[i - 1] === b[j - 1]) {
        matrix[i][j] = matrix[i - 1][j - 1];
      } else {
        matrix[i][j] = Math.min(
          matrix[i - 1][j] + 1, // deletion
          matrix[i][j - 1] + 1, // insertion
          matrix[i - 1][j - 1] + 1 // substitution
        );
      }
    }
  }

  return matrix[a.length][b.length];
}

With this, I can define a fuzzy match function:

function fuzzyMatch(str, query, maxDistance = 2) {
  return levenshtein(str.toLowerCase(), query.toLowerCase()) <= maxDistance;
}

Here, maxDistance defines how many “mistakes” we allow. For example, searching Haberfelner instead of Haberfellner still works, because the distance is just 1.

---

Applying Fuzzy Search to My Data

My app displays partners (companies with descriptions and tags). Before adding Levenshtein, search only worked for exact matches. After fuzzy matching, users can now find results even with typos.

For example, in my dataset:

{
  "name": "Haberfellner",
  "description": "Pravi mlin-najčistije brašno za najfinije pekarske proizvode.",
  "search": ["mlin", "brašno", "pekarski proizvodi"]
}

If someone searches for:

• habarfellner (typo in name)
• brasno (without diacritic)
• pekarskii proizvodi (extra i)

The fuzzy match still finds the right partner.

---

Generating Search Snippets

I also improved search results by generating snippets with highlighted matches:

function getSnippet(text, query, snippetLength = 50) {
  const cleanText = text.replace(/<[^>]*>/g, "");
  const lowerText = cleanText.toLowerCase();
  const index = lowerText.indexOf(query.toLowerCase());

  if (index === -1) return "";

  const start = Math.max(0, index - snippetLength);
  const end = Math.min(cleanText.length, index + query.length + snippetLength);
  let snippet = cleanText.substring(start, end);

  if (start > 0) snippet = "..." + snippet;
  if (end < cleanText.length) snippet = snippet + "...";

  const regex = new RegExp(`(${query})`, "ig");
  return snippet.replace(regex, "<b>$1</b>");
}

Now users see a short preview with their search term in bold.

---

Full Search Flow

1. Get the query from the request.

2. Normalize it (lowercase, trim).

3. Filter partners:

   • Exact match (includes).
   • Fuzzy match (fuzzyMatch).

4. Return results with highlighted snippets.

---

Example Search in Action

Searching for Yaraa (extra a) still matches Yara Italia, and searching for mlinsko braso still finds Haberfellner.

The result looks like this:

{
  "name": "Haberfellner",
  "slug": "haberfellner",
  "snippet": "...najčistije <b>brašno</b> za najfinije pekarske proizvode...",
  "tags": ["brašno"]
}

---

Conclusion

The Levenshtein algorithm is a simple but powerful tool for fuzzy search. By allowing small mistakes in spelling, it dramatically improves user experience. Combined with snippet previews and tag-based matching, it makes search far more forgiving and user-friendly.

Next step? Ranking results by relevance score (distance + tag priority) — but that’s a story for another post 😉.

---

Footnotes

1. In information theory, linguistics, and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences. The Levenshtein distance between two words is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one word into the other. It is named after Soviet mathematician Vladimir Levenshtein, who defined the metric in 1965. Wikipedia ↩